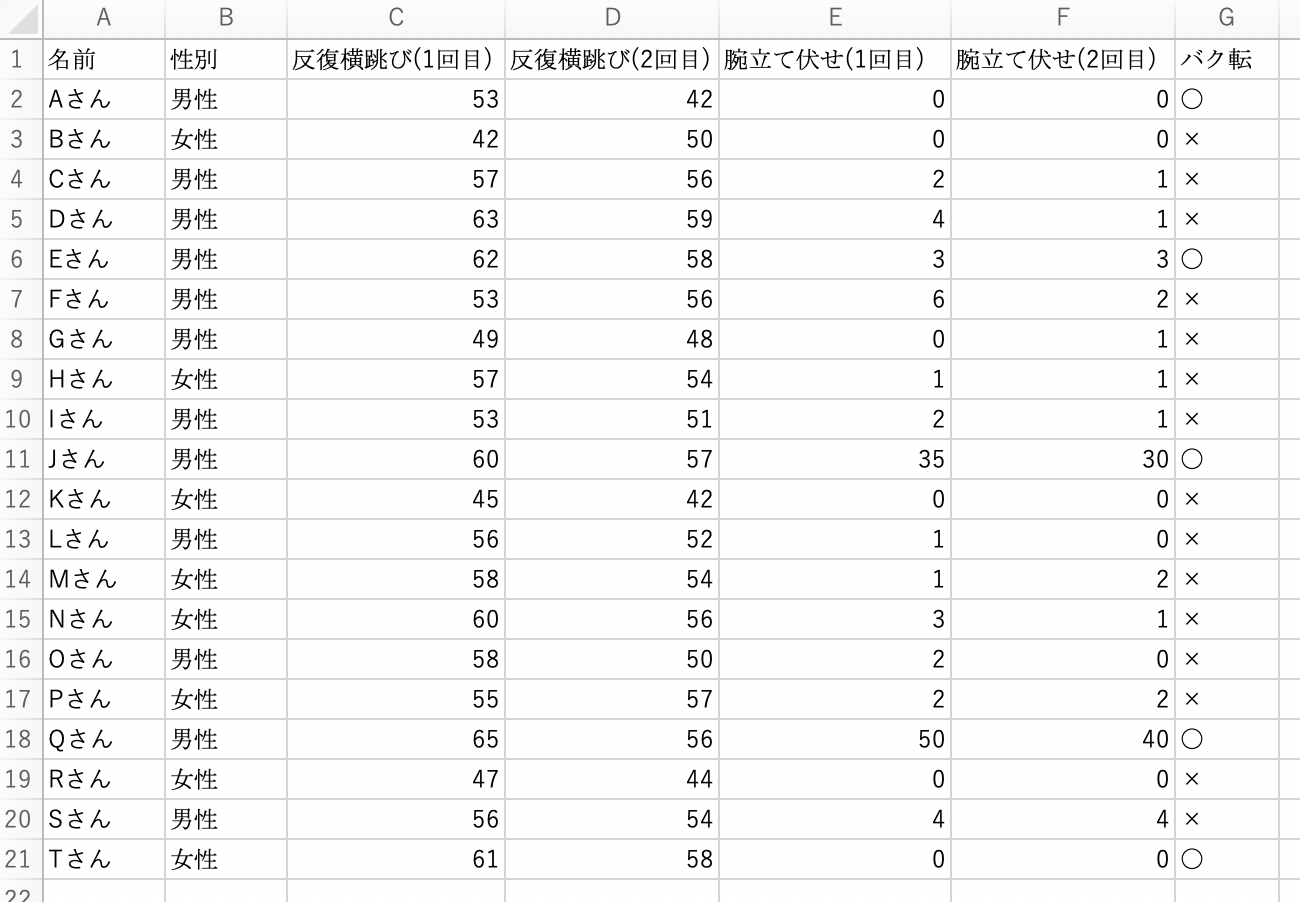
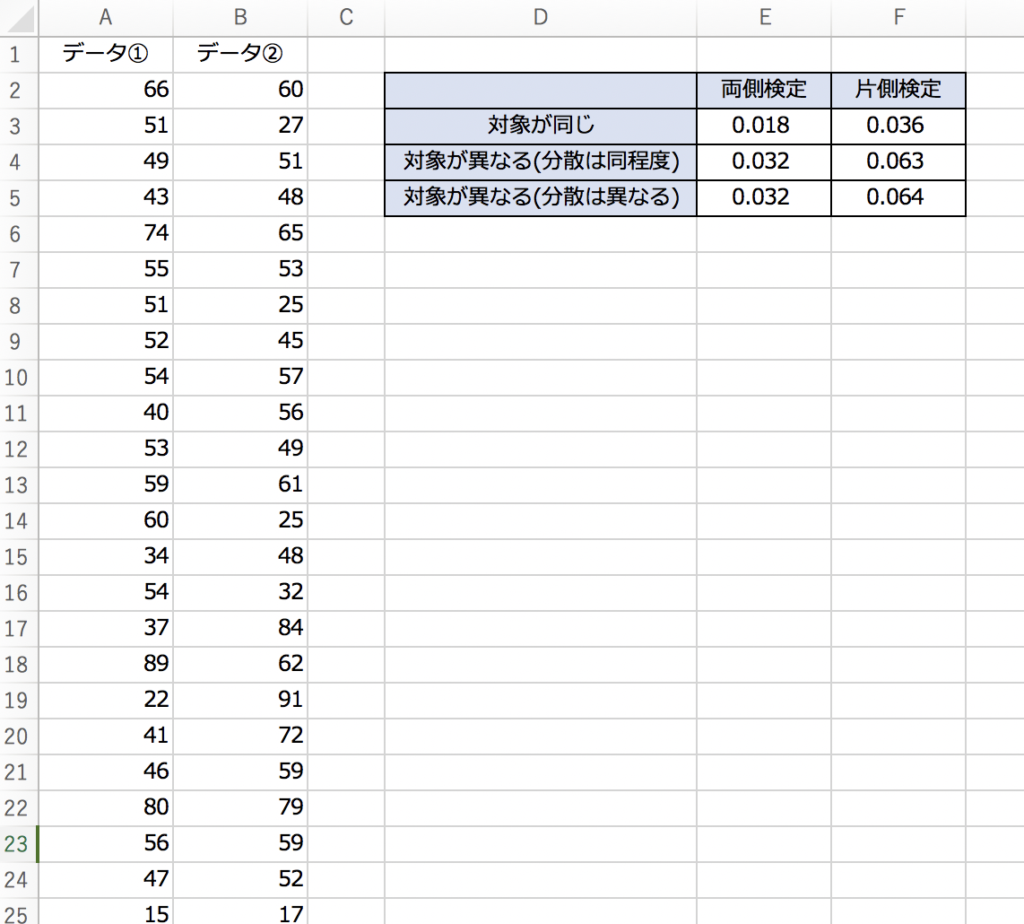
· ではいよいよ,マン・ホイットニーのu検定らしい作業に入っていきます. 統計量「U」を算出するため,以下のような式をセルに入れます. =(A5*A11)(A11*(A111)/2)D12マンホイットニーのU検定と何が違うの? T検定と何が違うの? さて、次回は「独立した2群間の連続変数を比較する」統計解析でノンパラメトリック検定である MannWhitney U 検定 (マンホイットニーU検定)について説明します。でu検定を紹介している。また,類似の記述は最近のテキストの中にも認め られる(例えば森, 1999 。特に岩原(1984)の著書は本邦における推測統 計学の古典的名著であり,教育・心理学分野のみならず医

Roc曲線のためのサンプルサイズ計算 エクセルでサンプルサイズ Hha Shop
マンホイットニーのu検定 エクセル アドイン
マンホイットニーのu検定 エクセル アドイン- · マン・ホイットニーのU検定 ノンパラメトリック (=パラメータに制限が一切ない)な統計学的検定の一つであり、特に特定の母集団がもう一方よりも大きな値を持つ傾向にある時に、「2つの母集団が同じである」とする帰無仮説に基づいて検定する。 独立な2組の標本の有意差検定として用いられる。 つまり標本数(母集団の数)がバラバラな集団の有意差を証明する · マン・ホイットニーのU検定 2つの集団のサンプルサイズが、n1、n2である場合以下のような検定統計量を算出します。 $$U_1=n_1n_2\frac{n_1(n_11)}{2}R_1$$ もしくは $$U_2=n_1n_2\frac{n_2(n_21)}{2}R_2$$ R 1 とR 2 はそれぞれの順位の総和です。 この内の小さな方の値を使います。



Pythonによる仮説検定の実行方法 データサイエンス情報局
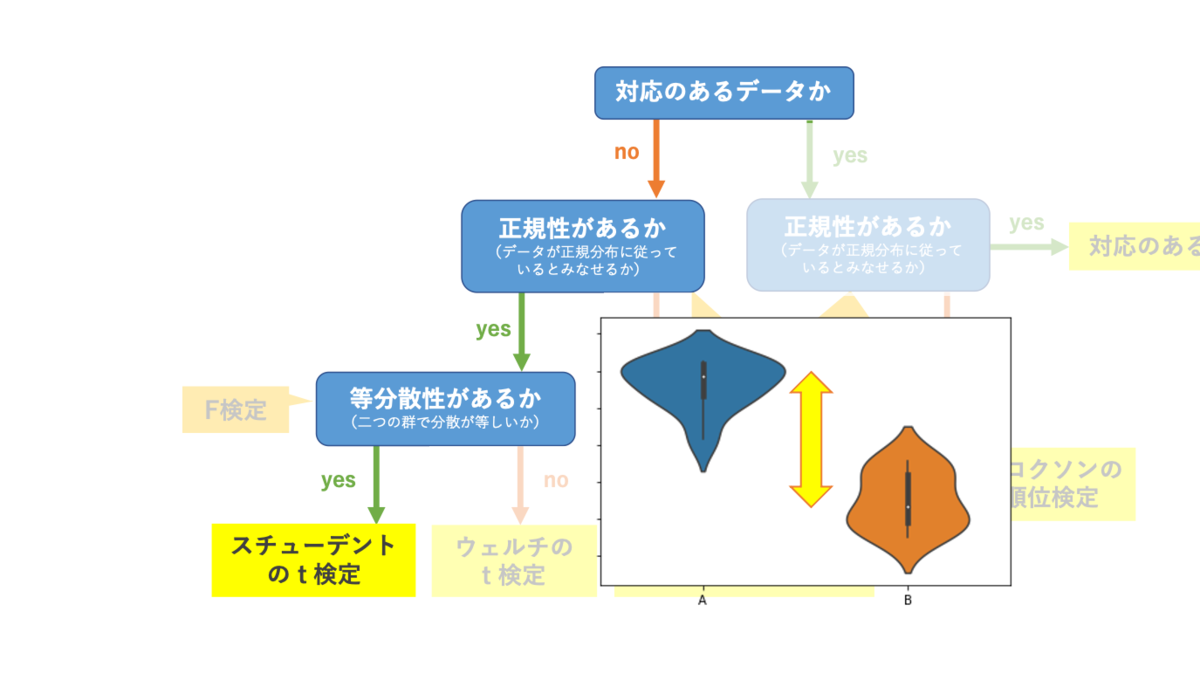
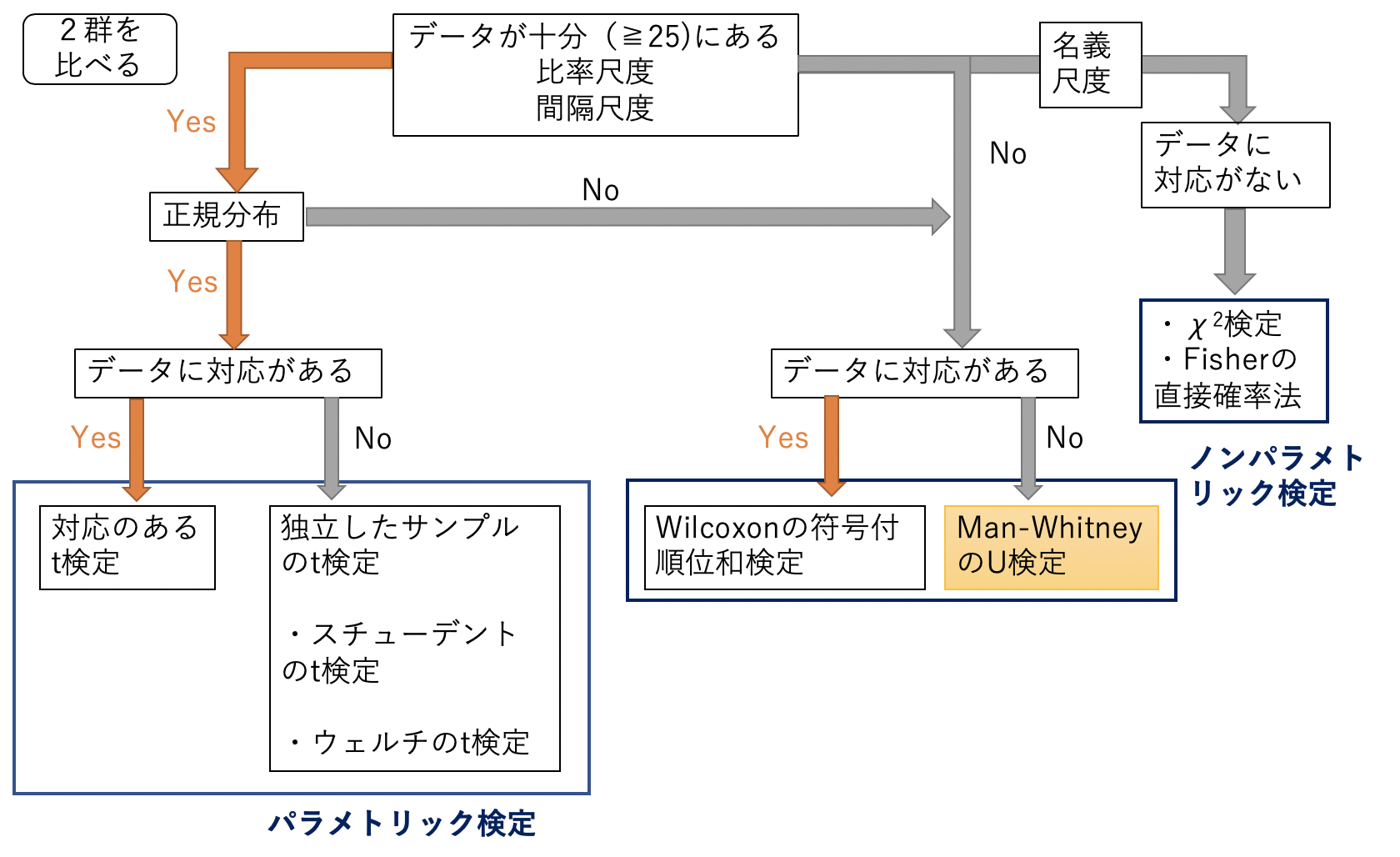
EZRでマンホイットニーのU検定を実施するのに使用するデータ ということで、今回の記事で使うデータです。 今回はA群、B群の2つの群で、LDHの平均値を比較してみます。 (データは架空のデータです。 ) 実際には、T検定で実施したときと同じデータをT検定をしたいけど データが正規分布とは言えない場合 •2つのクラスを比べるような(対応のない)場合 →マンホイットニーのU検定 •同じテストを2回受けたような(対応のある)場合 →ウィルコクスンの符号付順位和検定ステューデントのt検定 対応のあるステューデントのt検定 一元配置分散分析 テューキーの方法 ダネットの方法 ウィリアムズの方法 ノンパラメトリック検定 スピアマンの相関係数 マン・ホイットニーのU検定 ウィルコクソンの順位和検定
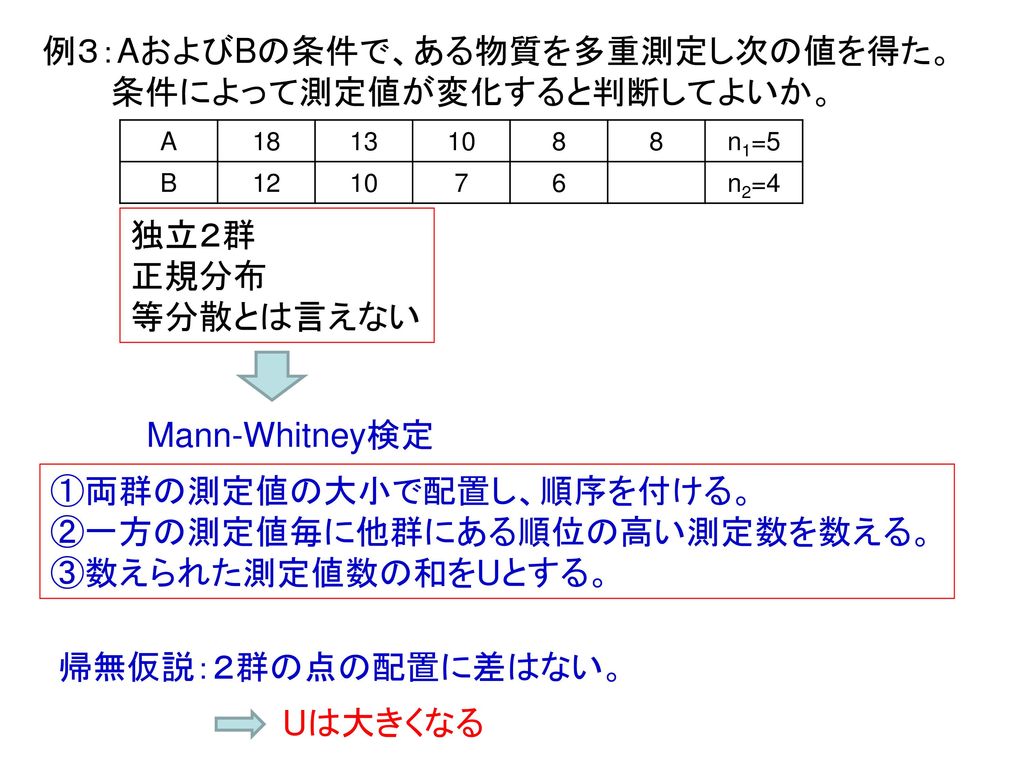
適当な指標である 統計量u を計算し、その指標が起こる確率を計算 両群に統計学的に「意味がある&有意'差」があるかどうかを検討 ボヱヹベアチテドヺのu検定 a,b まとめて順位を付ける。 その順位 · マン・ホイットニーのu検定と不等分散時における代表値の検定法 名取真人 岡山理科大学理学部動物学科 はじめに マン・ホイットニーのu 検定(ウィルコク ソン・マン・ホイットニー検定)は,対応の ない2群の検定法であり,正規性の仮定を必 要としない。直接的な方法では、各カメを順番にとり、それぞれが負かしたウサギの数を数えると、こうなる: 6, 1, 1, 1, 1, 1。 したがって U = 6 1 1 1 1 1 = 11。 間接的な方法では: 各カメの順位の合計は1 7 8 9 10 11 = 46になる。
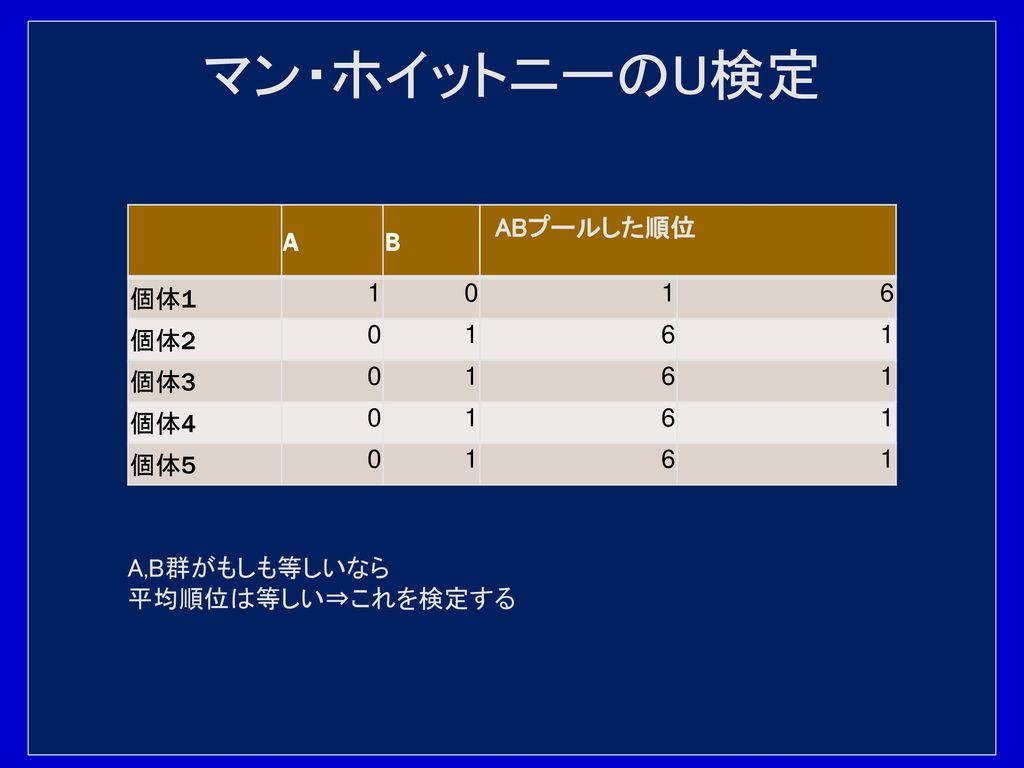
Wilcoxonの順位和検定(マン・ホイットニーのU検定) (原データを用いることができます) 手法の説明 ・使用法 ・in English それぞれの群のサンプルサイズを記入してください(半角)。 サンプルサイズはそれぞれ1000まで可能です。 その下の大きな枠に、それぞれの群のデータをコンマまたはスペースで区切って下の枠内に記入してください。 縦書きでも横書きで例題では, 第 1 群に属する観察値に付けられた順位の和 R1 =1346 =14 R 1 = 1 3 4 6 = 14 第 2 群に属する観察値に付けられた順位の和 R2 =257=31 R 2 = 2 5 7 8 9 = 31 となる。 検定統計量 U 1 U 1 , U 2 U 2 を求める。 U 1= n1 n2 n1 (n11) 2 −R1 U 1 = n 1 n 2 n 1 ( n 1 1) 2 − R 1 U 2= n1 n2 n2 (n21) 2 −R2 U 2 = n 1 n 2 n 2 ( n 2 1) 2 − R 2計算式 MannWhitney検定では、正規近似法を使用して検定のp値を算定します。 は、平均値0および標準偏差1、N (0,1)のほぼ正規分布に従います。 3つの対立仮説の正規近似p値で、連続量修正値05を使用します。 データに同順位が含まれていると、Z 統計量より




パラメトリック 検定 論文でよく使う統計手法 検定の選び方や一覧のまとめ




ヤフオク 3251 Ssri エクセル統計10
· この検定は,まず American Cyanamid という会社の Wilcoxon(ウィルコクソン)という人が1945年に,1標本の場合(Wilcoxon の符号付き順位検定)と2標本の場合(この方法)の考え方を提案し,1947年に Mann(マン)と Whitney(ホイットニー)が U という統計量を導入しシステム上のエラーが発生しました。 システム上に不備がある、つまりプログラムやファイルに関してのエラーです。 こちら側のプログラム上の不備が原因であるため、 お手数ですが、 TOPページ から メールにてどの手法で、又マン・ホイットニーのU検定 まん・ほいっとにーのゆーけんてい MannWhitney U test 仮説検定 かせつけんてい ウイルコクソンの符号順位検定 ういるこくそんのふごうじゅんいけんてい ウイルコクソンの順位和検定 ういるこくそんのじゅんいわけんてい ラページの検定 らぺーじのけんてい ふたつ




大学生協ソフトウェアインフォメーション




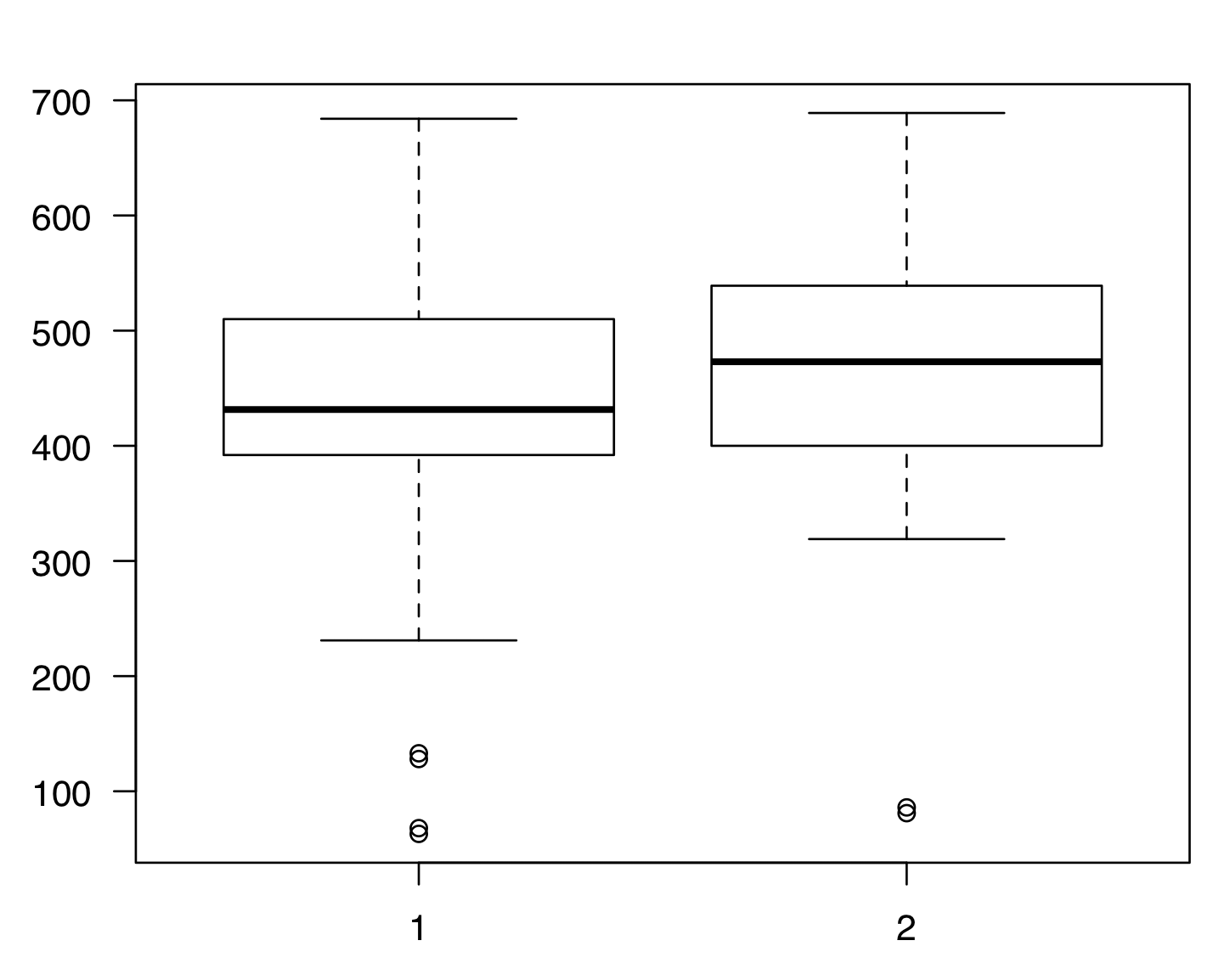
Boxplot 独学で始める統計 データサイエンス
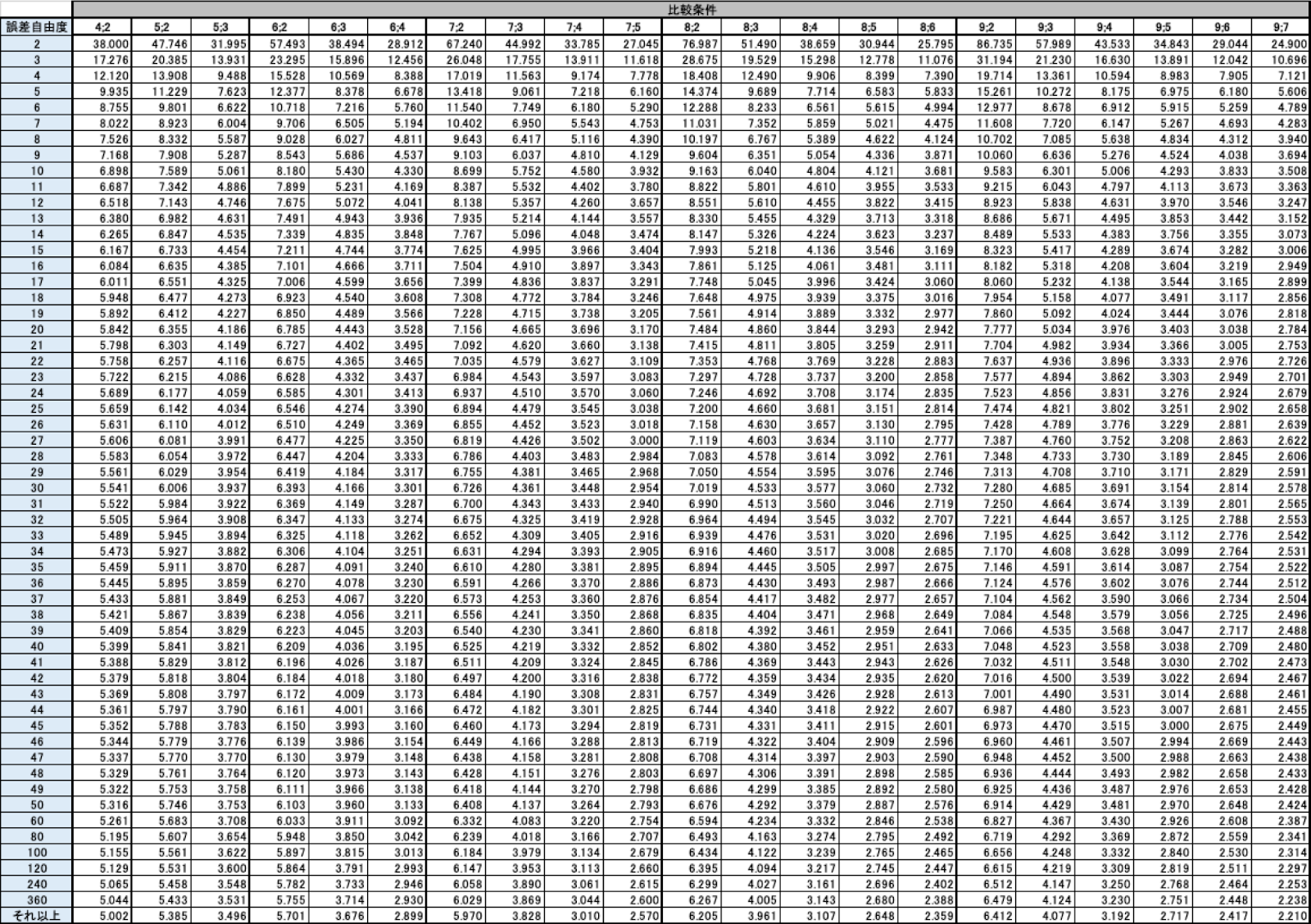
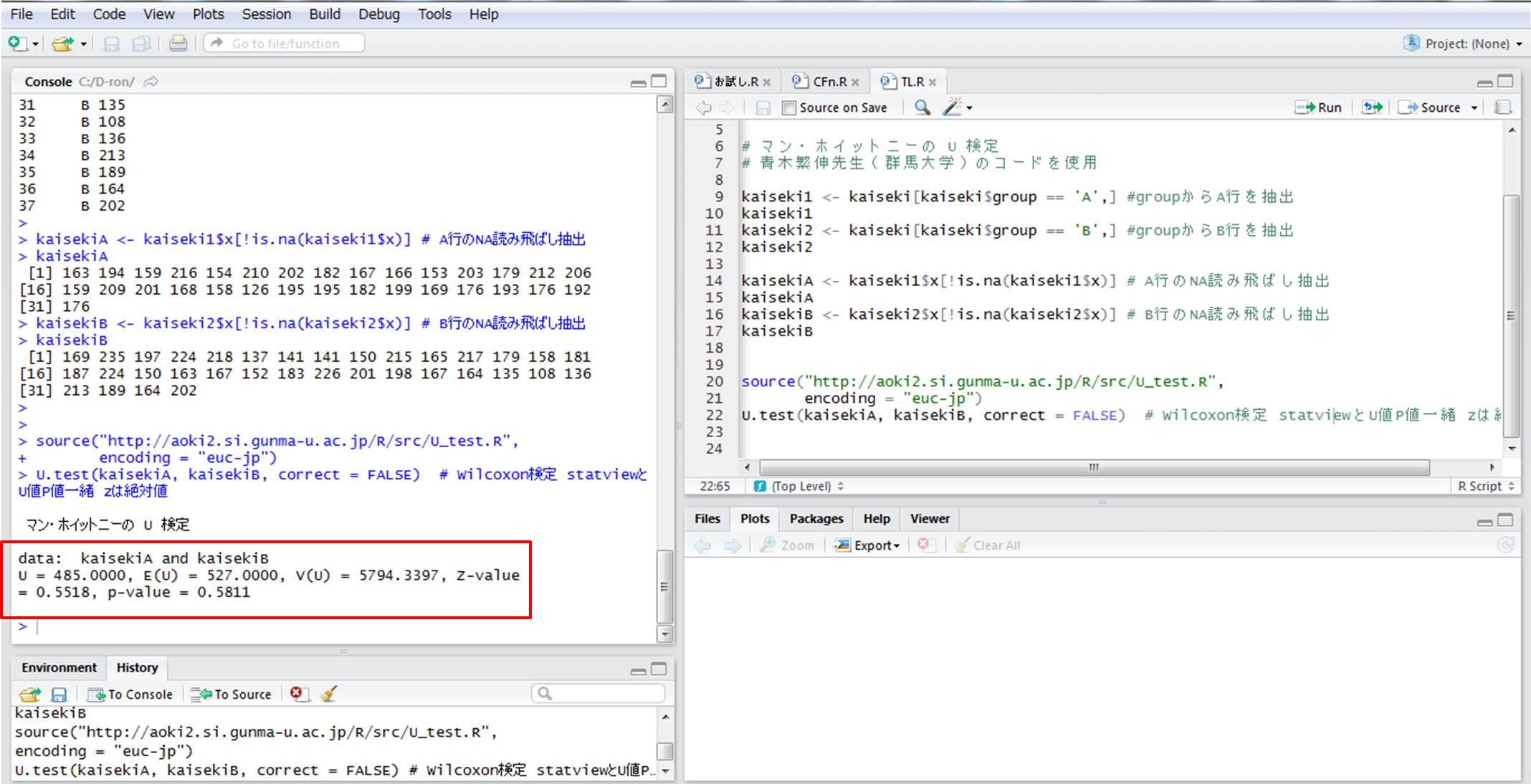
2つのMannWhitneyのUの計算 • この後の計算で用いるU値を算出する • 2つのグループをA、Bとして、ケース数を n1,n2とすると、グループAのU(U1)の計算 式は • もう一つのU2は、 • U1>(n1×n2)÷2のときはU2を、それ以 外のときはU1をMannWhitneyのUとして扱 う 115統計量Uを求める。 この場合では大腸がんの群に注目してU値を求める。 U値は次のようになる。 U値 = 2+2+3 +5 = 125 n 1 ≦かつn 2 ≦なので、 MannWhitney検定表 よりU値がそれ以上極端となる確率Pを求める。 n 1 =6、n 2 =8のときの両側確率P<005となるU値の下側有意点は8である。 計算したU値は8よりも大きいので、P≧005となり帰無仮説を棄却できない目的 マン・ホイットニーの U 検定を行う (R には,等価な検定を行う関数 wilcoxtest が用意されている) 使用法 二つのデータベクトルを与えるとき Utest(x, y, correct=FALSE) Utest(x, y) 2 行 k 列の分割表を与えるとき Utest(x, correct = FALSE) Utest(x) 引数 x 第一群の観測値ベクトルまたは,分割表データ(y



スチューデントのt検定の概要とpython実装 実践ケモインフォ




Roc曲線のためのサンプルサイズ計算 エクセルでサンプルサイズ Hha Shop
マンホイットニーのU検定を行うマクロ マンホイットニーのU検定におけるU統計量と標準Z得点を計算します。 データ数を返す関数length()も用意されています。 標準Z得点は同順位がある場合に対応していません。 Excelワークシートをダウンロードノンパラメトリック手法 マンホイットニーのU検定を分かりやすく解説しますt検定の代わりです ノンパラメトリック手法 マンKeyword ノンパラメトリック, 検定 概要 本サンプルはマン・ホイットニー(Mann Whitney)のU検定を行うサンプルプログラムです。 本サンプルは以下に示される2つの独立した標本を分析対象とし、検定統計量U、P値等を算出します。




ウィルコクソンの順位和検定とは マンホイットニーのu検定との違いは いちばんやさしい 医療統計



データ解析のサポート ヒューマン メタボローム テクノロジーズ株式会社
· マンホイットニーのU検定について教えてください。 詳しい方にご教授いただきたく投稿させていただきました。 非正規分布で等分散である対応のない2群について マンホイットニーのU検定を行ったところ、5%水準で有意差が出ました。 · 13 t検定とMann WhitneyのU検定 2 まとめ 正規分布しているかどうかで使うべき検定法などが変わる まずはこの表を見てください。 連続変数 を扱う場合には、その変数が 正規分布(パラメトリック)かそうでないか で使うべき検定法などが変わります · エクセル(E統計)でやるマンホイットニーのU検定 検定手法の概要です。 マンホイットニーのU検定は対応のない中央値の差の検定を行うノンパラメトリック検定 です。 では、「対応なしデータ」の基本統計量の表を見ながら、どこにマンホイットニーのU検定が適用できるか確認していきましょう。 ノンパラメトリック検定なのでn数はとくに関係はありません




保健統計演習 1 橋本 永吉 新井 Ppt Download



第9回 二標本ノンパラメトリック検定 例1 健常者8人を30分間ジョギングさせ その前後で血中の Ppt Download
111 マン-ホイットニーのU検定 独立した2組の標本が属している母集団の分布が等しいかどうかを検定するノンパラメトリック手法。 検定手順: 帰無仮説 h 0 :「2 群の母代表値に差はない」。 対立仮説 h 1 :「2 群の母代表値に差がある」。KruskalWallis 検定は,2群以上の代表値の差の検定であり,2群の場合,MannWhitney U 検定に等しい。この検定には,近似検定と正確検定があり,どちらが使われるか区別が必要である。Keyword ノンパラメトリック, 検定 概要 本サンプルはマン・ホイットニー(Mann Whitney)のU検定を行うC言語によるサンプルプログラムです。 本サンプルは以下に示される2つの独立した標本を分析対象とし、検定統計量U、P値等を算出します。



順位和検定について Excel エクセル で学ぶデータ分析ブログ



Ezrの使い方 マン ホイットニー検定 U検定 気楽な看護 リハビリlife
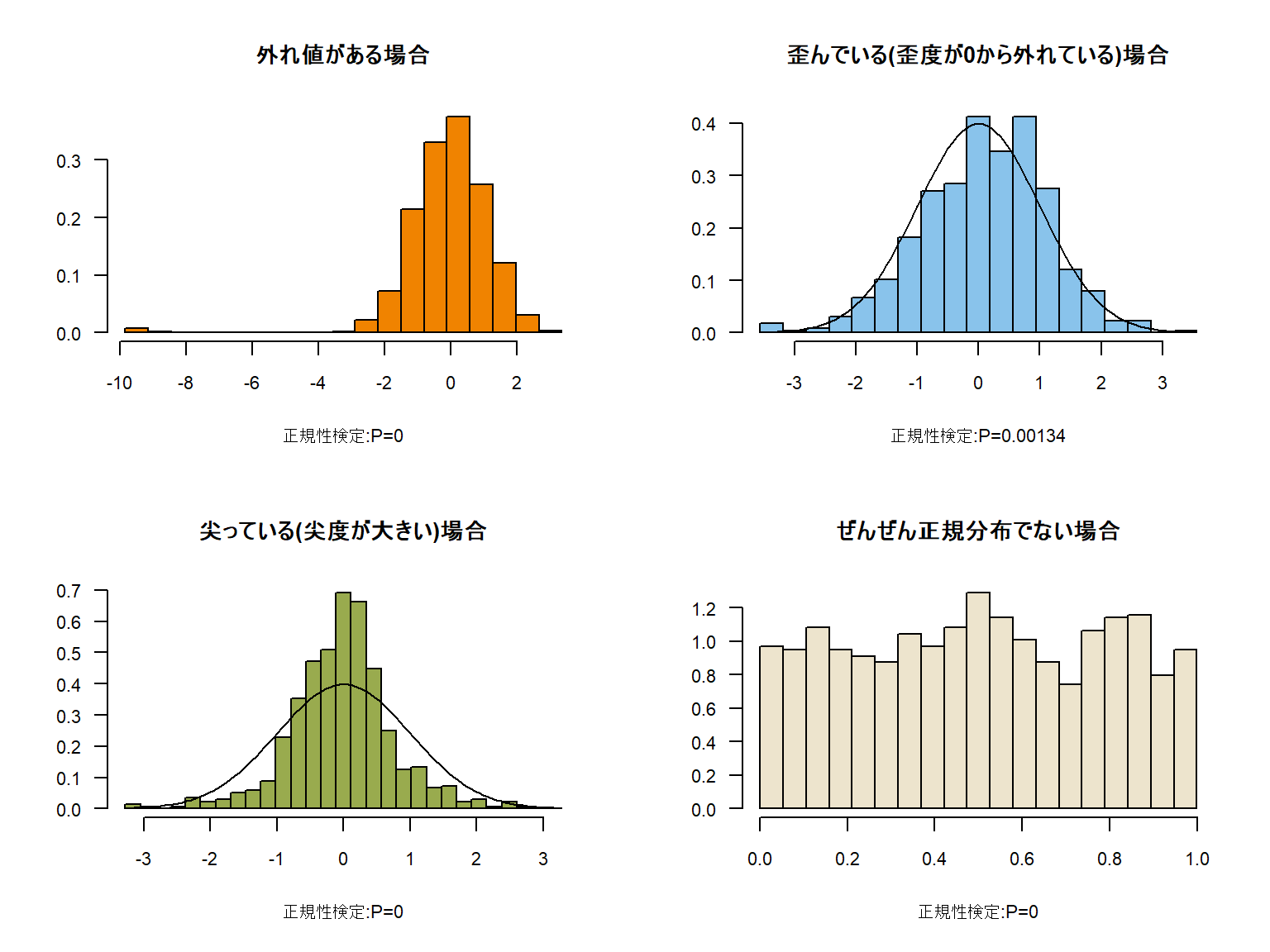
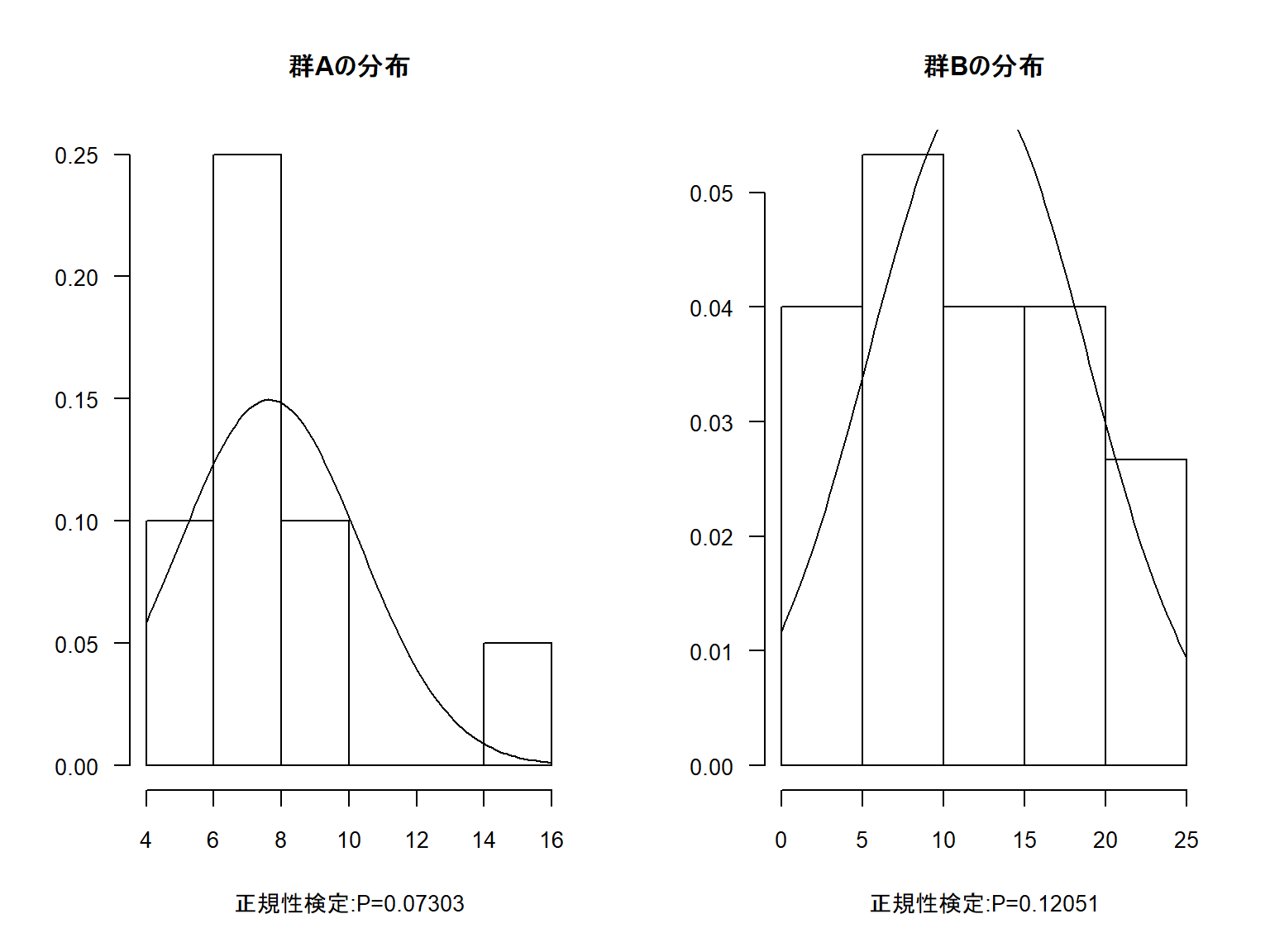
マン・ホイットニーのu検定 😩 正規分布を示すサンプルなら、~30のサンプル数があれば検定上差し支えない それ以下でも問題ない場合もある とか、正規分布でないサンプルは最低6~8のサンプル数が必要とか、厳密さを要求される調査であれば50くらいのサンプル数が必要であろうとかです。




T 検定メインページ Ultrabem トップページ




Statmate V 日本スリービー サイエンティフィック




Pythonによる仮説検定の実行方法 データサイエンス情報局



最も検出力が高いとされる多重比較 テューキー ウェルシュ法をエクセルで算出する




書籍情報 Excelデータ分析 増補版




ライブ配信セミナー ノンパラと多変量解析入門 12月8日 火 開催 主催 株 シーエムシー リサーチ Cmcリサーチのプレスリリース
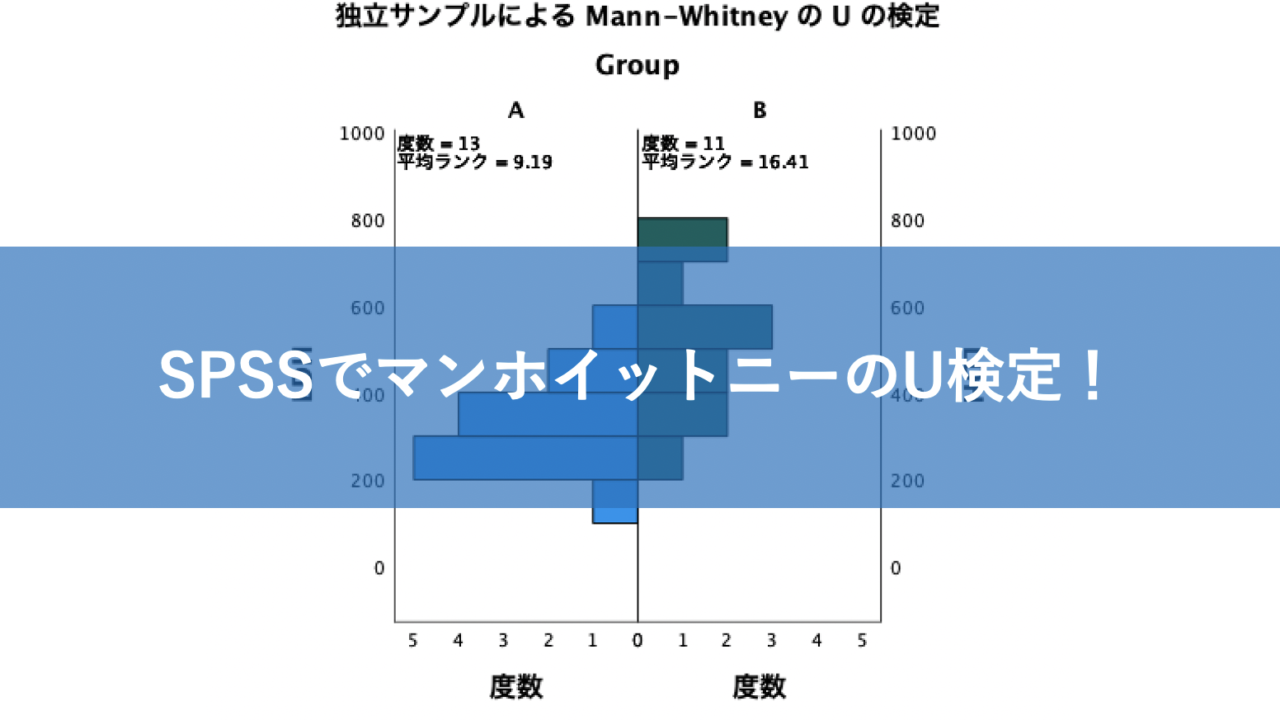



Spssでマンホイットニーのu検定を実施する方法 いちばんやさしい 医療統計




マン ホイットニーのu検定 少しp値 シティプランナー見習いのブログ



ウィルコクソンの符号順位検定 Wilcoxon Signed Rank Test Japaneseclass Jp



Rの統計メモ




連続変数の解析 ステューデントのt検定とマン ホイットニーのu検定 保健師ジャーナル 75巻7号 医書 Jp



迅速 高度なデータ処理 集計 検定 プラスワンリサーチ




食事パターン分析のための食事コーディング アプローチについて アイルランドの研究 文献紹介 みんな栄養に頼りすぎてる



Mbaheblogjpgrnh 選択した画像 箱ひげ図 有意差 書き方 箱ひげ図 有意差 書き方



5 13 3限 連続変数の比較と検定 4 2 On Vimeo
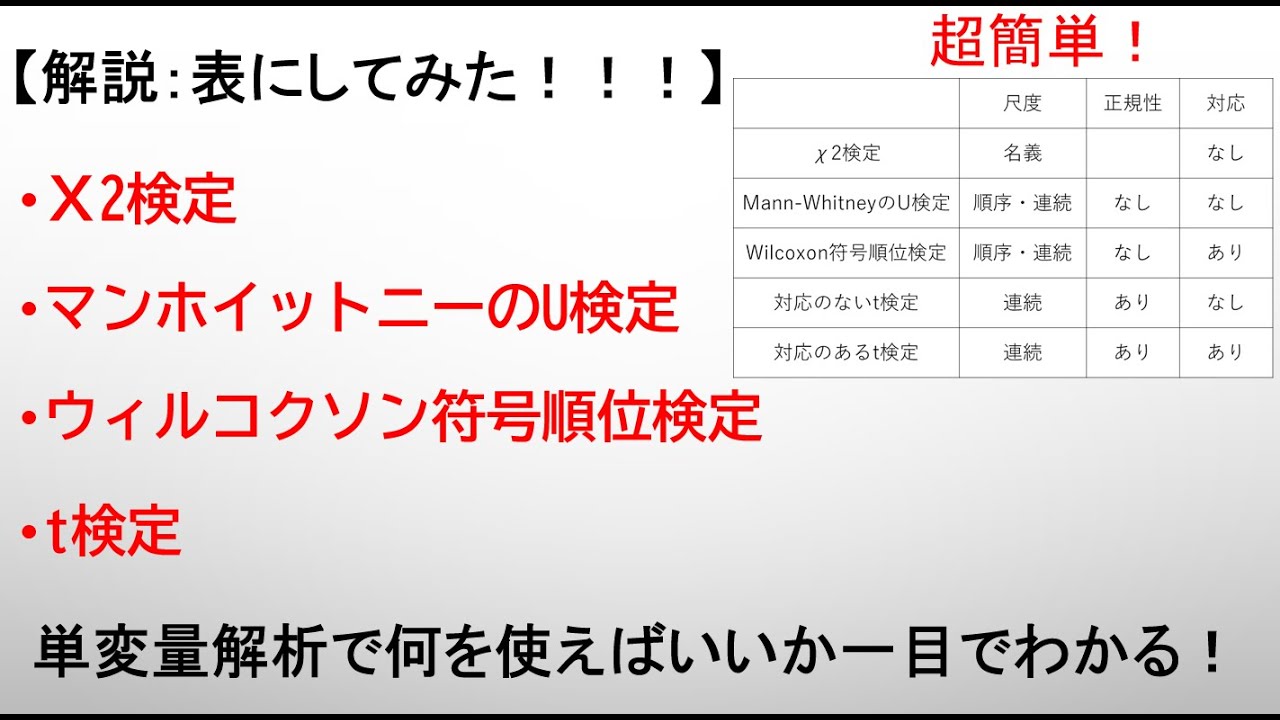



解説誰でもわかる X2検定 マンホイットニーのu検定 ウィルコクソン符号順位検定 t検定の違いを表にしてみた 卒論 論文で使える知識 ー単変量解析編ー Youtube




タイがあるため 正確な P 値を計算することができません に対しての Wilcox Test Wilcox Testの設定方法 Qiita




眼圧下降を目的としたアイリーアによるnvg治療 治療戦略 Rvo Eylea Jp
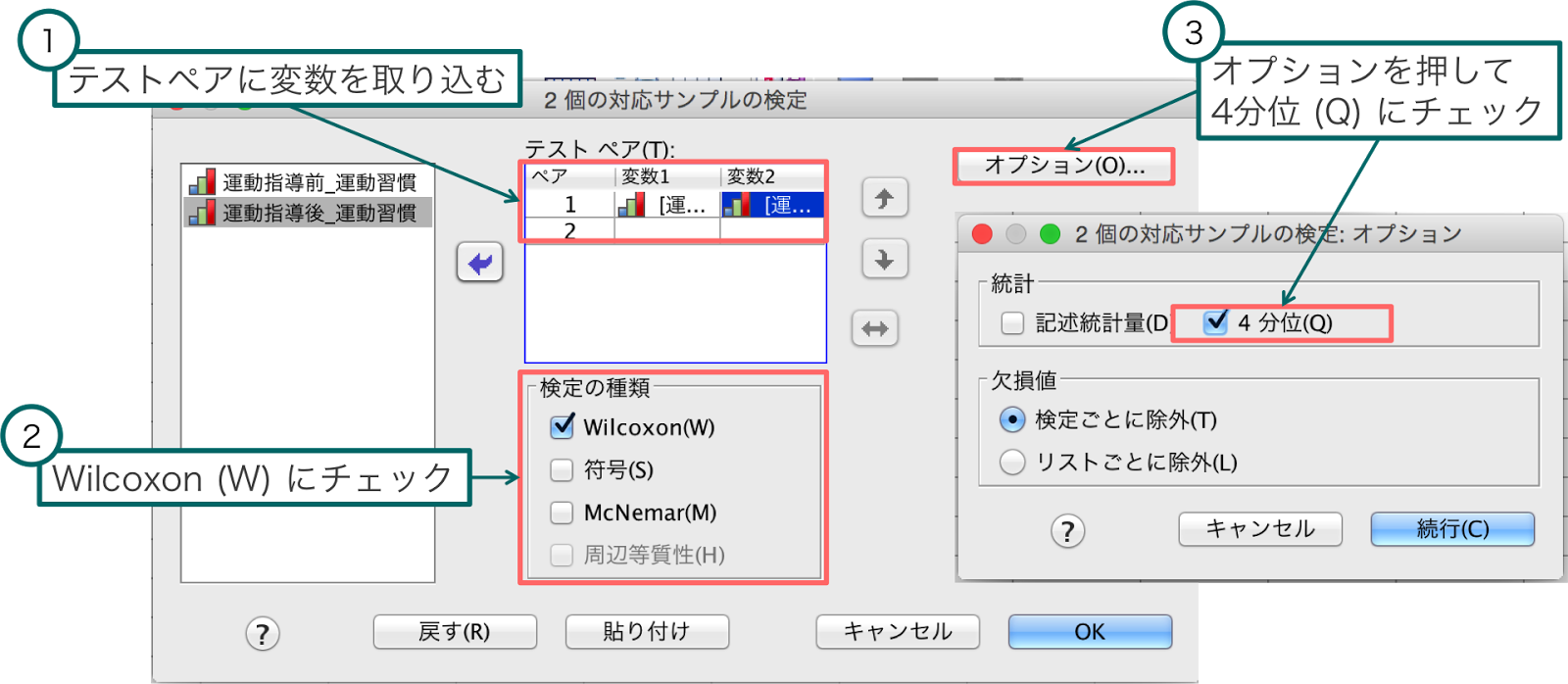



ウィルコクソンの符号順位検定 Wilcoxon Signed Rank Test Japaneseclass Jp




論文を正しく読み書くためのやさしい統計学 改訂第3版 中村 好一 本 通販 Amazon



Ezrの使い方 マン ホイットニー検定 U検定 気楽な看護 リハビリlife
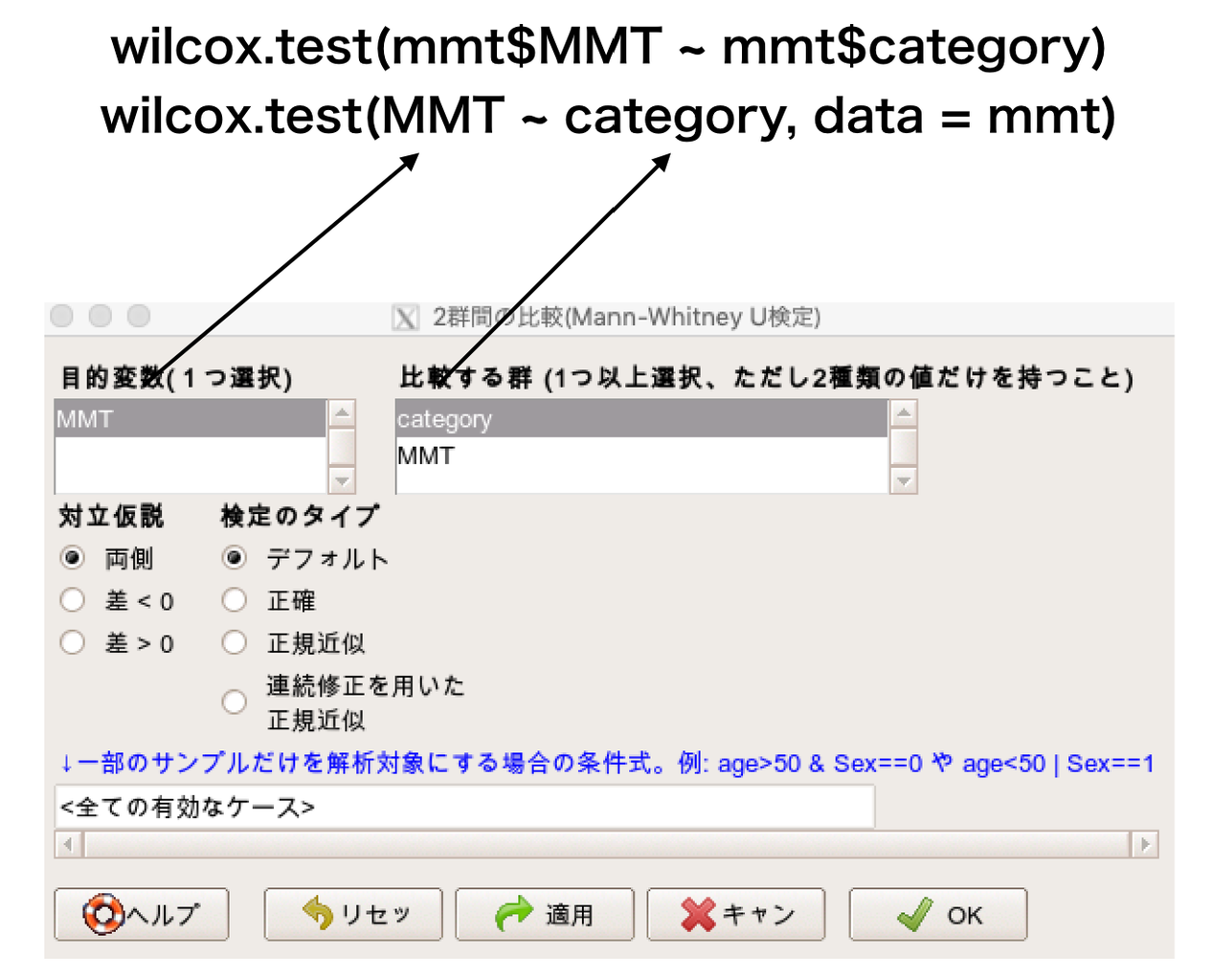



Boxplot 独学で始める統計 データサイエンス



保健統計演習 橋本 Ppt Download




マン ホイットニーのu検定 サンプルサイズ計算 エクセルでサンプルサイズ Youtube



大阪市立大学 大学院医学研究科 医療統計学教室




統計の勉強 多群比較の時の効果量ってどうやって計算するの Eiko Programming Note




Spssで統計解析のお手伝いをします 素人でもわかるspss統計




メディカルスタッフのためのひと目で選ぶ統計手法 目的 と データの種類 で簡単検索 適した手法が76の事例から見つかる 結果がまとめられる 羊土社




マン ホイットニーのu検定 サンプルサイズ計算 エクセルでサンプルサイズ Youtube



順位和検定について Excel エクセル で学ぶデータ分析ブログ
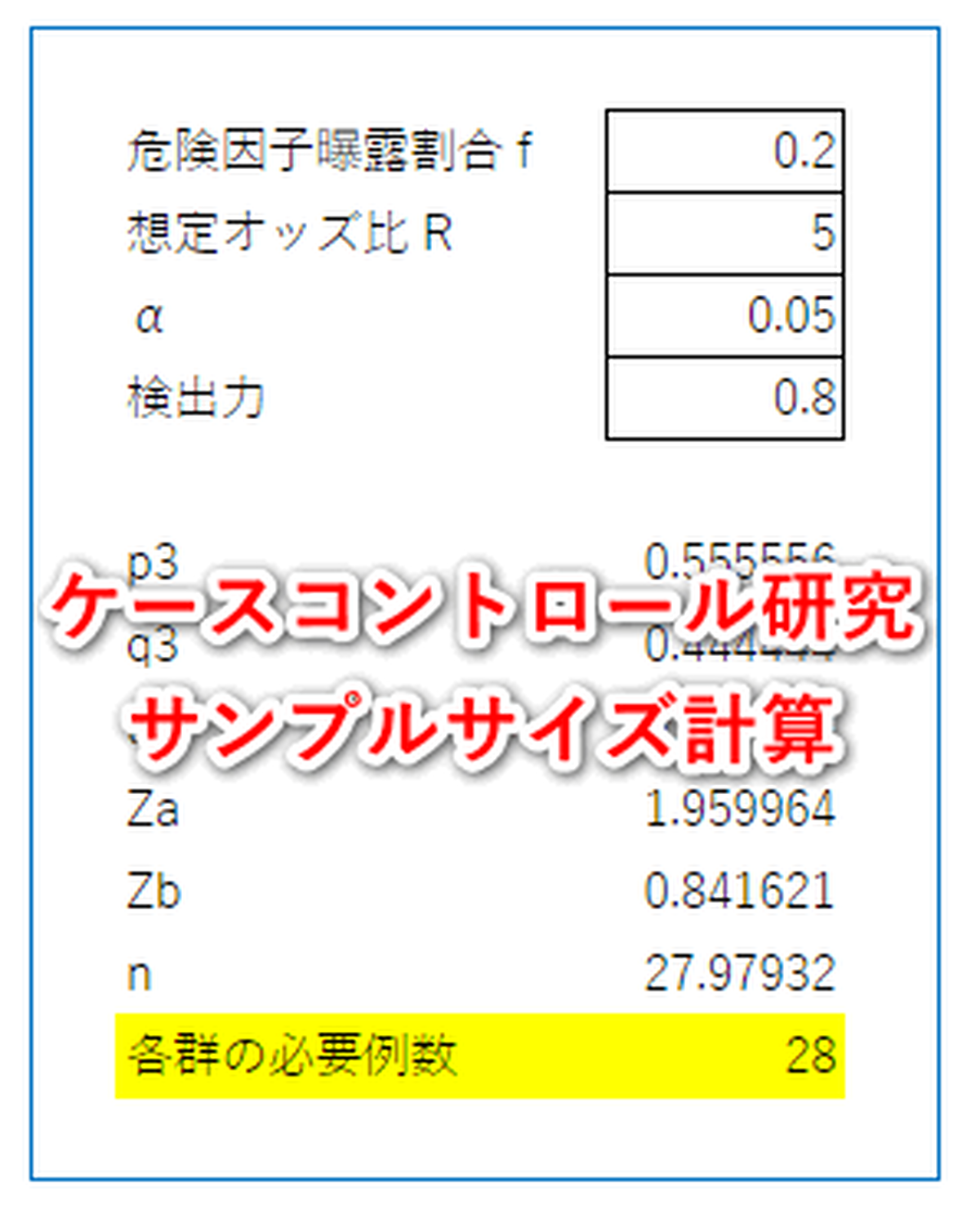



疫学 ケースコントロール研究 サンプルサイズ計算 エクセルでサンプルサイズ Hha Shop
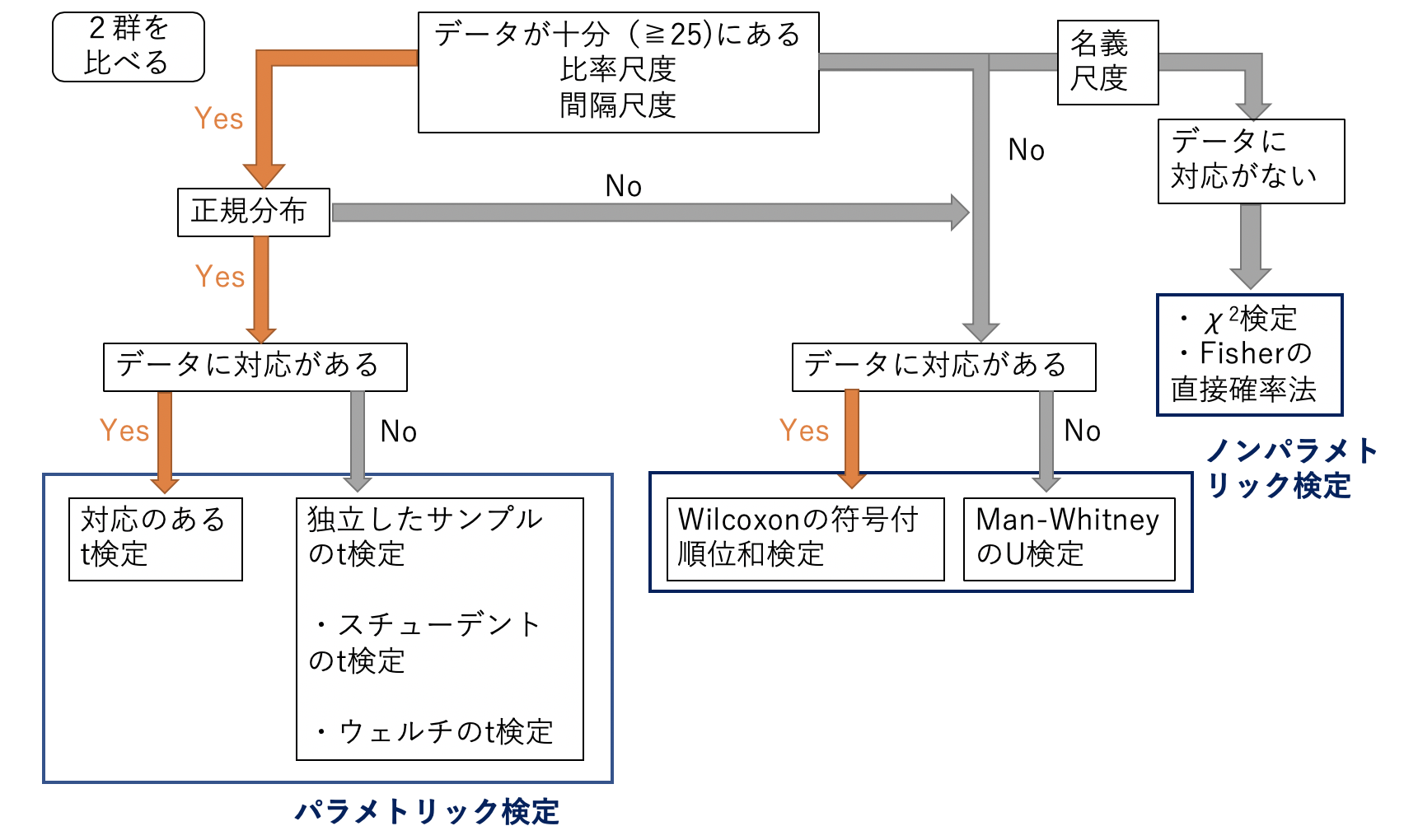



統計学入門 2群の差の検定 検定方法の選び方 気楽な看護 リハビリlife




統計 Wilcoxonの順位和検定とマンホイットニーのu検定 こちにぃるの日記
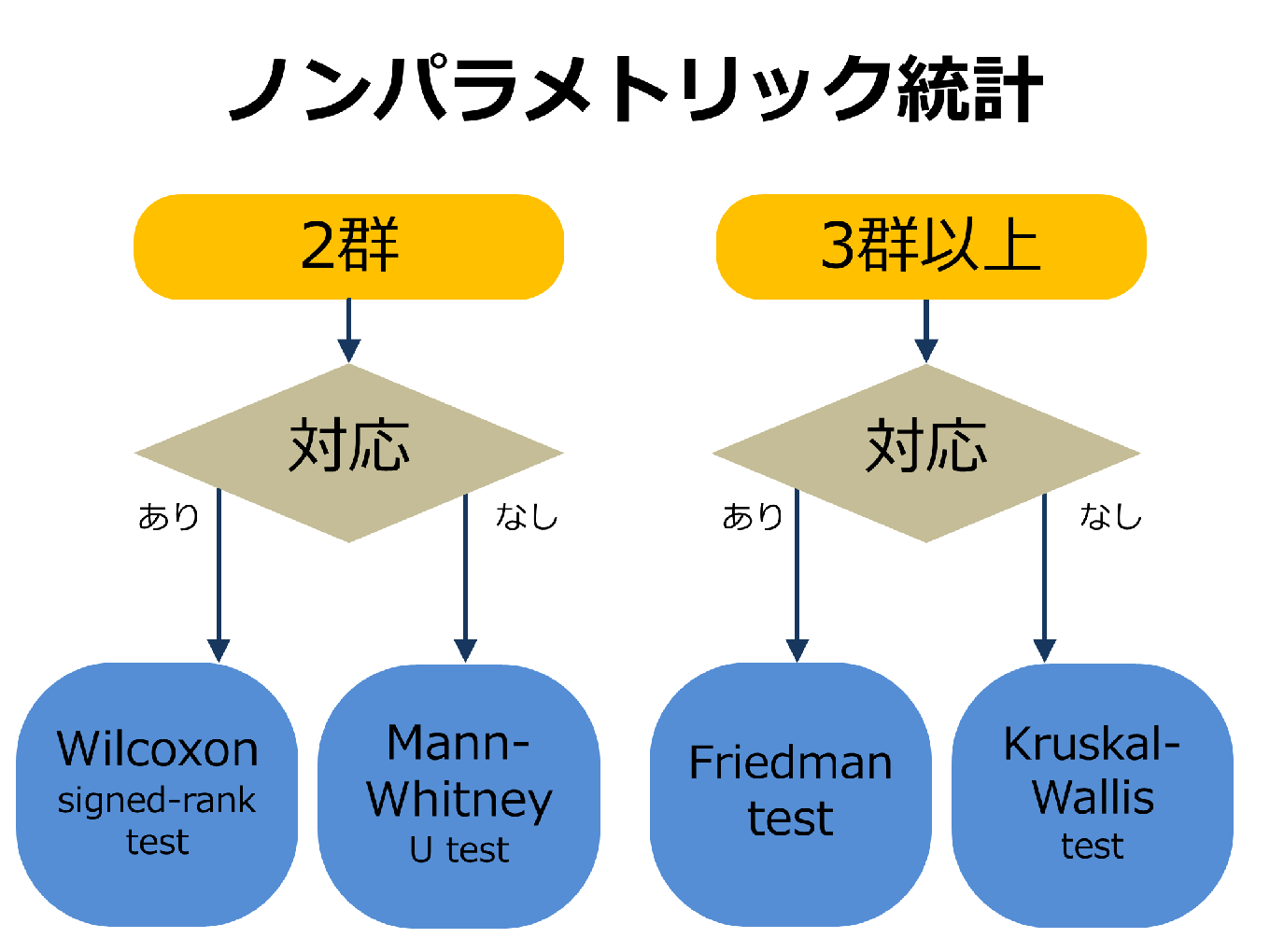



論文でよく使う統計手法 検定の選び方や一覧のまとめ




Js Starの練習帳 32 5 ノンパラメトリック法 2 データに対応がない場合 Nakano Hiroyuki Note




Android 用の Stats Tester 簡単統計検定 Apk をダウンロード




ライブ配信セミナー ノンパラと多変量解析入門 4月9日 金 開催 主催 株 シーエムシー リサーチ Cmcリサーチのプレスリリース
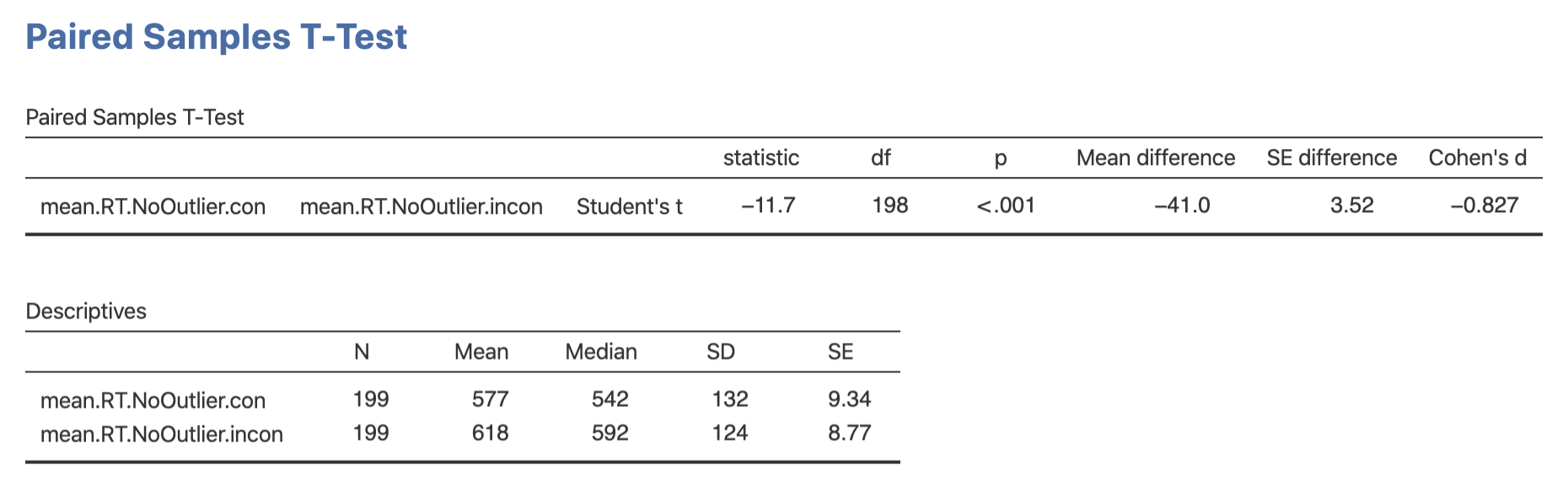



4 平均値の検定 Jamovi ガイドブック 北星学園大学版




外れ値 Wikipedia



Ezrの使い方 マン ホイットニー検定 U検定 気楽な看護 リハビリlife




Ezrでmann Whitney U 検定を行う方法 深kokyu
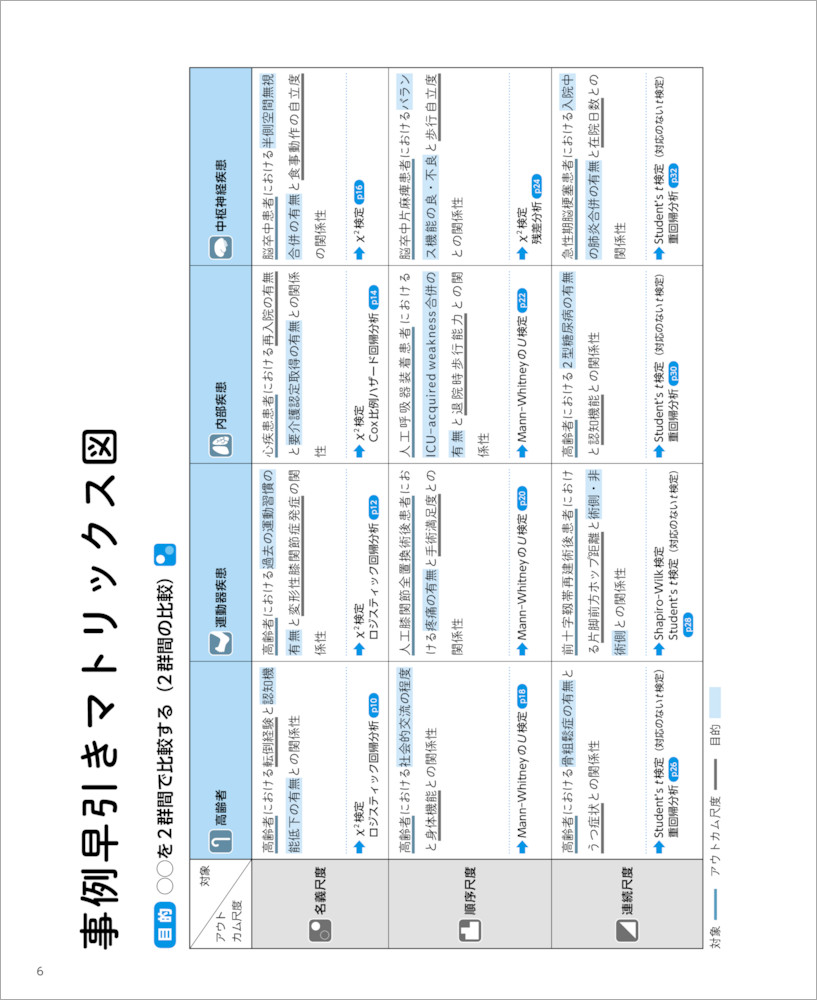



メディカルスタッフのためのひと目で選ぶ統計手法 目的 と データの種類 で簡単検索 適した手法が76の事例から見つかる 結果がまとめられる 羊土社
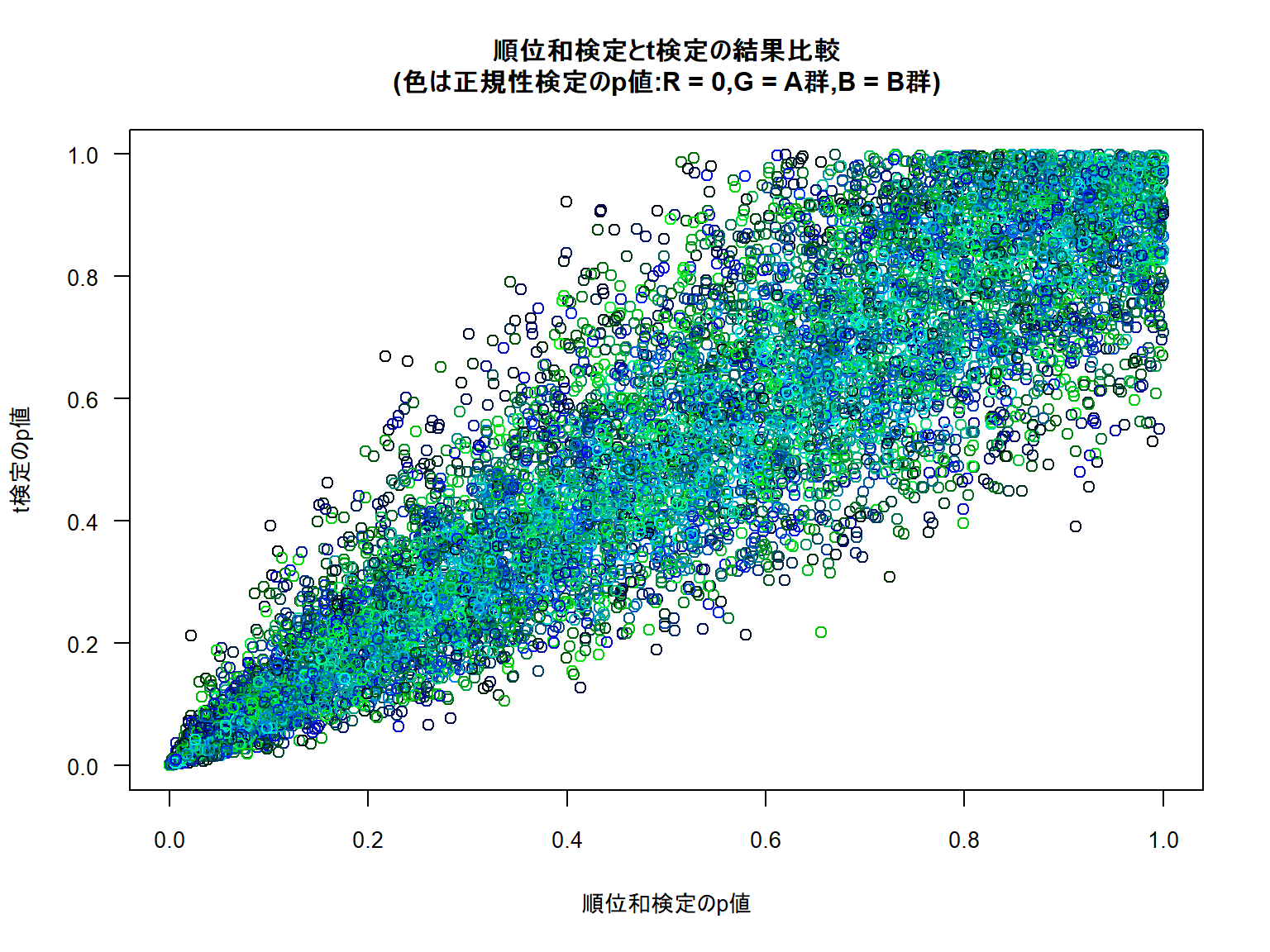



順位和検定について Excel エクセル で学ぶデータ分析ブログ
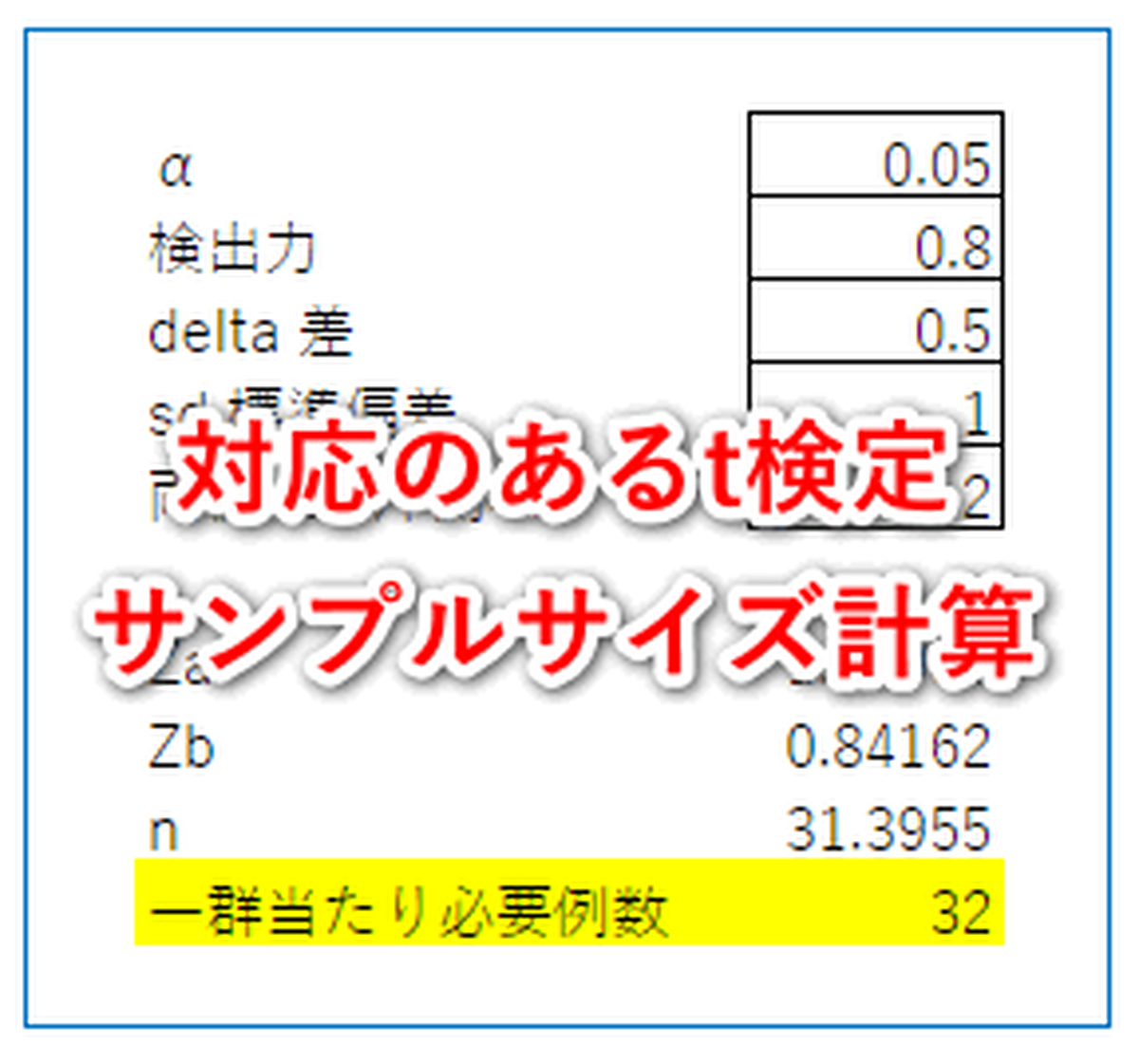



対応のあるt検定 サンプルサイズ計算 エクセルでサンプルサイズ Hha Shop




割合の差の検定 割り付け比にも対応 サンプルサイズ計算 エクセルでサンプルサイズ Hha Shop




12 号 タモギタケ抽出物を有効成分とする抗カンジダ菌剤ならびにカンジダ症予防および または治療剤 Astamuse
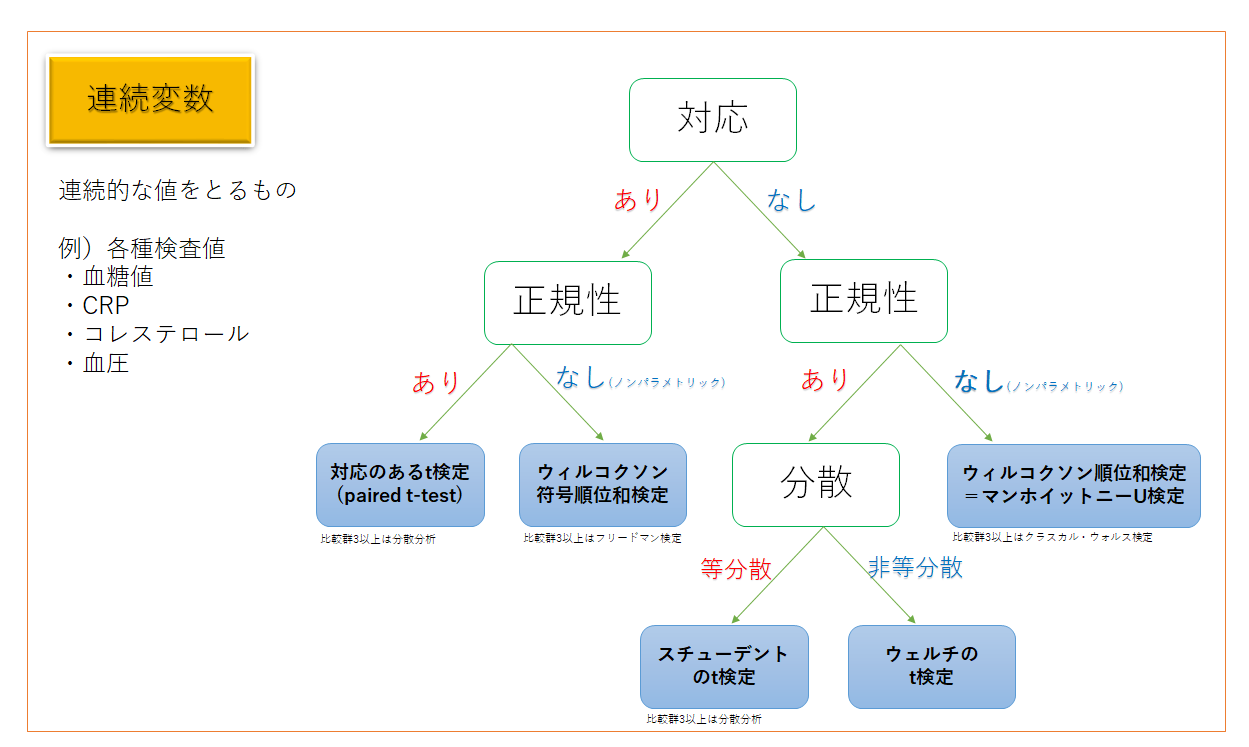



パラメトリック 検定 論文でよく使う統計手法 検定の選び方や一覧のまとめ




Wo10 号 慢性ストレスの評価方法 Astamuse



表計算ソフトで行うwilcoxonの検定 医療情報学
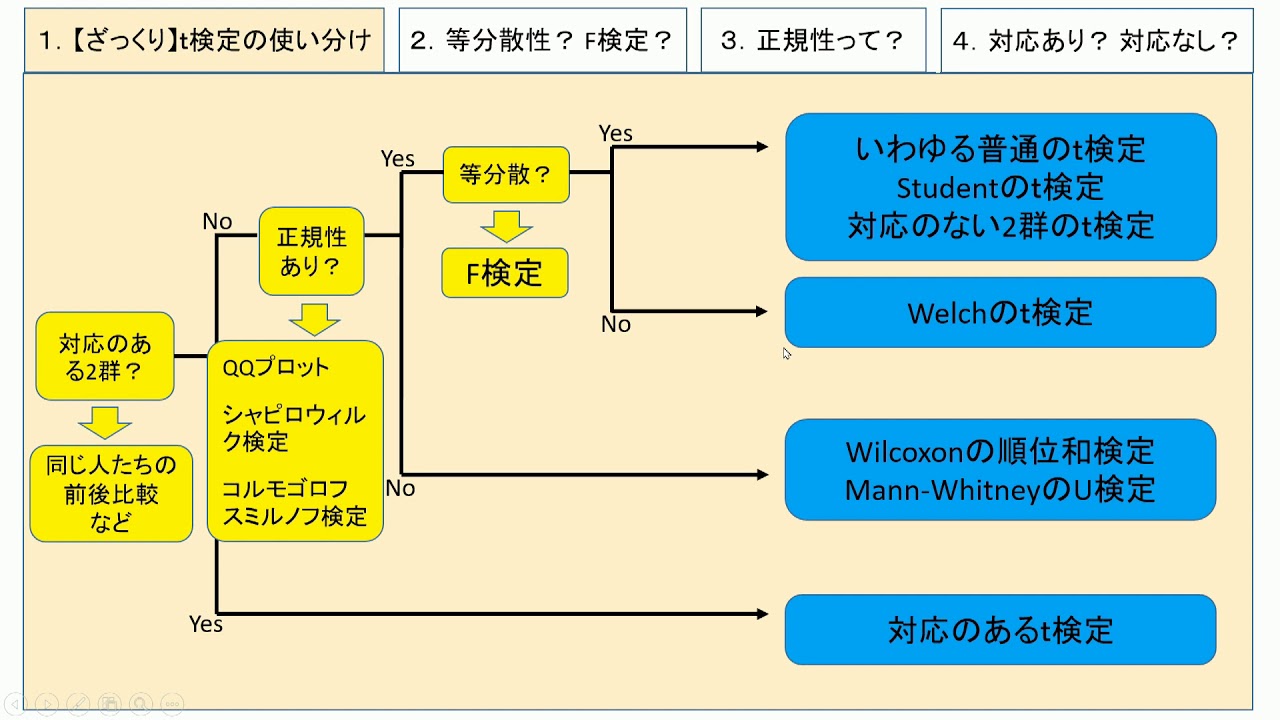



Spssで実際にt検定をやってみる 操作 結果の見方 t検定の使い分け Youtube
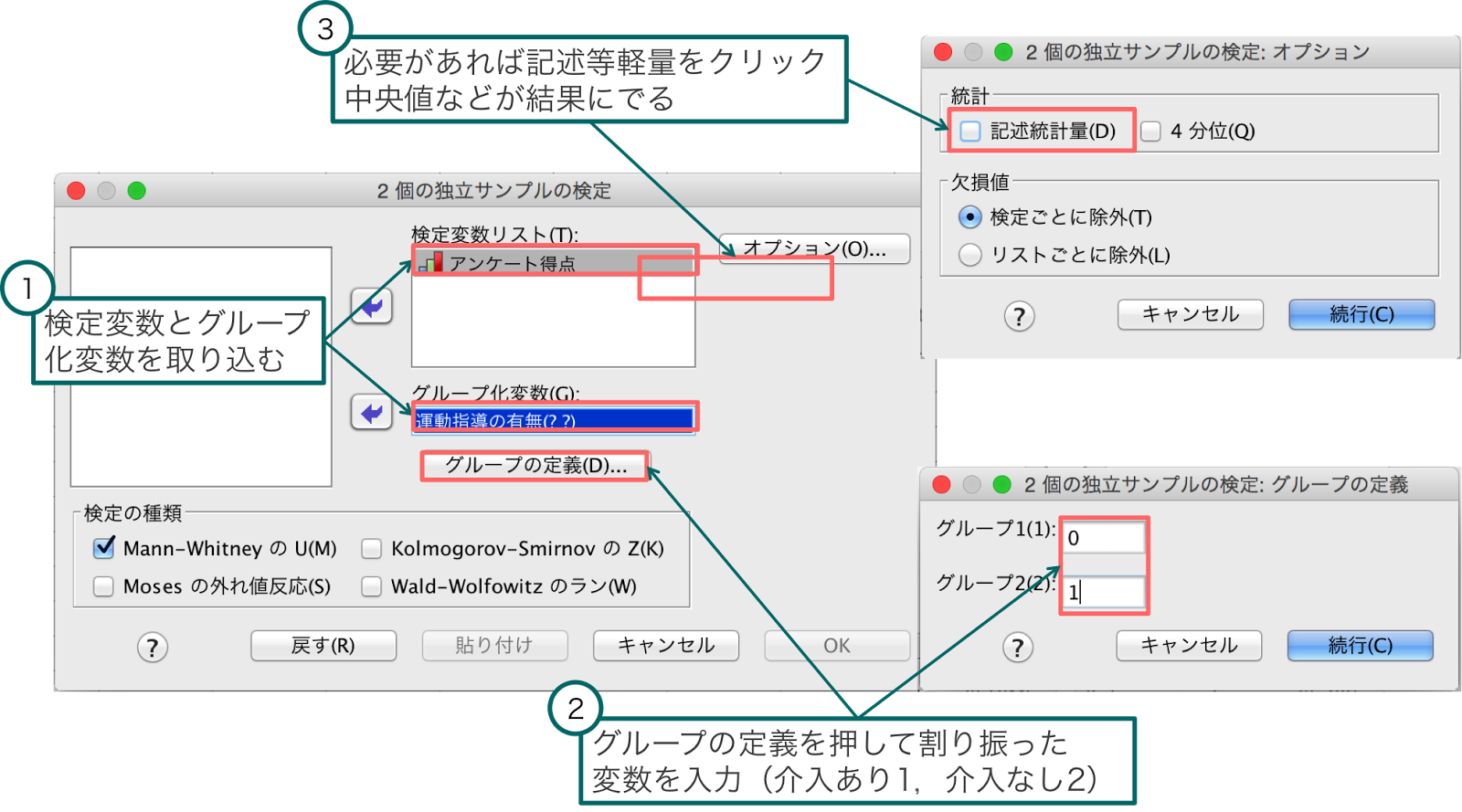



Mann Whitneyのu検定 Study Channel




統計 クラスカル ウォリス検定 Kruskal Wallis Test こちにぃるの日記



マン ホイットニー の U 検定 Mann
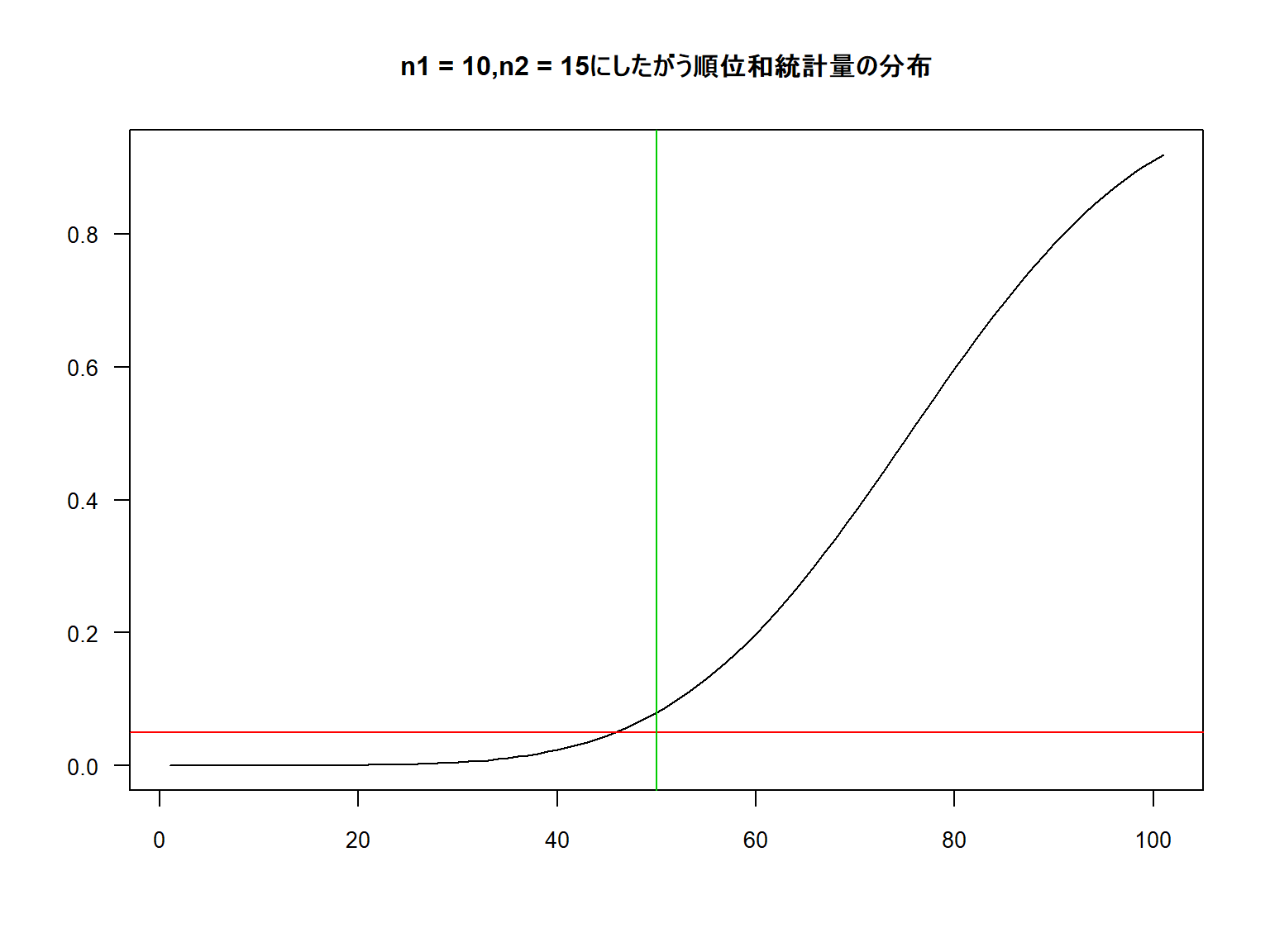



順位和検定について Excel エクセル で学ぶデータ分析ブログ




生物統計学 第7回 違いを調べる 3 カイ二乗検定 Ppt Download




マン ホイットニー の U 検定 Mann




Ezrでt検定を行う方法 深kokyu



マン ホイットニー の U 検定 Mann
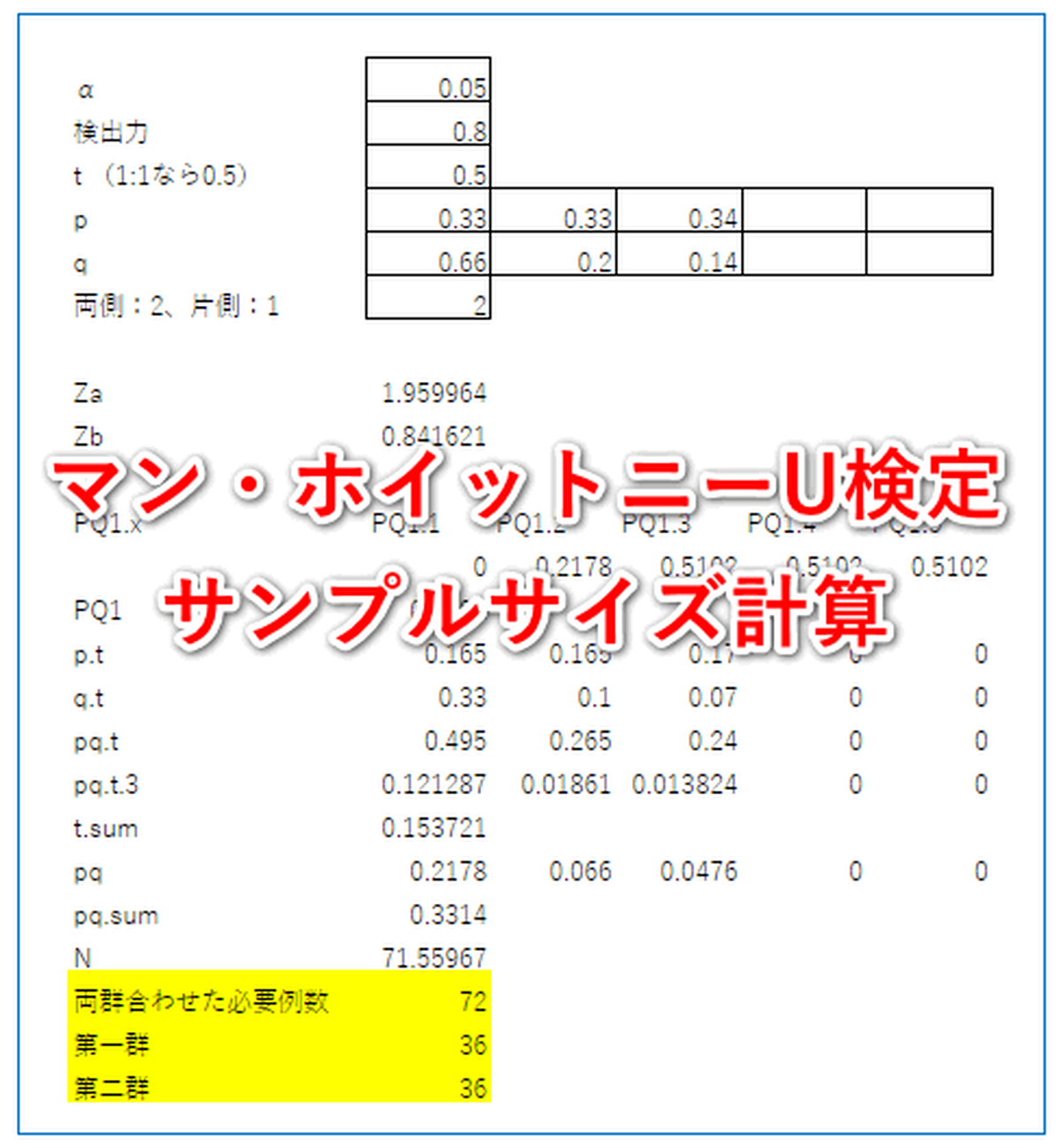



マン ホイットニーのu検定 サンプルサイズ計算 エクセルでサンプルサイズ Hha Shop



0 件のコメント:
コメントを投稿